Indices¶
Indices in SeqAn allow efficient pattern queries in strings or sets of strings. In contrast to, e.g., online-search algorithms that search through the text in \(\mathcal{O}(n)\), substring indices find a pattern in sublinear time \(o(n)\).
Indices store additional data structures that allow searching the text using an iterator. Using the iterator can be thought of as traversing a suffix tree. The following section gives you an introduction how the suffix tree is built.
Tip
The Finder interface allows searching indices without using the iterator. For more information check out the tutorial on Indexed Pattern Matching.
Suffix Trees¶
We consider an alphabet Σ and a sentinel character $ that is smaller than every character of Σ. A suffix tree of a given non-empty string s over Σ is a directed tree whose edges are labeled with non-empty substrings of s$ with the following properties:
1. Each outgoing edge begins with a different letter and the outdegree of an internal node is greater than 1. 2. Each suffix of s$ is the concatenation of edges from the root to a leaf node. 3. Each path from the root to a leaf node is a suffix of s$.
The following figure shows the suffix tree of the string s=”mississippi” (suffix nodes are shaded):
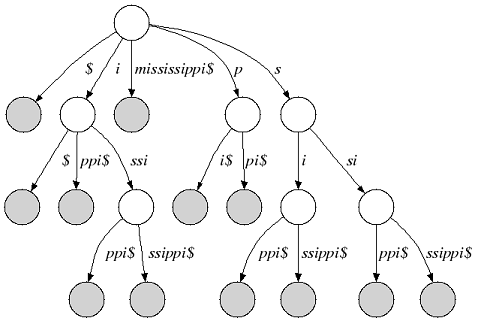
Figure 1: Suffix tree of “mississippi”
Many suffix tree construction algorithms expect $ to be part of the string alphabet which is undesirable for small bit-compressible alphabets (e.g. DNA). In SeqAn there is no need to introduce a $. We relax suffix tree criterion 2. and consider the relaxed suffix tree that arises from the suffix tree of s by removing the $ character and all empty edges. In the following, we only consider relaxed suffix trees and simply call them suffix trees. In that tree a suffix can end in an inner node as you can see in the next figure (suffix “i”):
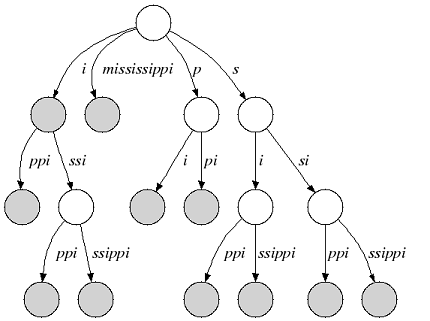
Figure 2: Relaxed suffix tree of “mississippi”