Pairwise Sequence Alignment¶
- Learning Objective
You will learn how to compute global and local alignments, how you can use different scoring schemes, and how you can customize the alignments to fulfill your needs.
- Difficulty
Average
- Duration
1h
- Prerequisites
Alignments are one of the most basic and important ways to measure similarity between two or more sequences. In general, a pairwise sequence alignment is an optimization problem which determines the best transcript of how one sequence was derived from the other. In order to give an optimal solution to this problem, all possible alignments between two sequences are computed using a Dynamic Programming approach. Scoring schemes allow the comparison of the alignments such that the one with the best score can be picked. Despite of the common strategy to compute an alignment, there are different variations of the standard DP algorithm laid out for special purposes.
We will first introduce you to the global alignments. Subsequent, you will learn how to compute local alignments. Finally, we will demonstrate how you can reduce the search space using a band.
Global Alignments¶
In this section, we want to compute a global alignment using the Needleman-Wunsch algorithm. We will use the Levenshtein distance as our scoring scheme.
A program always starts with including the headers that contain the components (data structures and algorithms) we want to use.
To gain access to the alignment algorithms we need to include the <seqan/align.h> header file.
We tell the program that it has to use the seqan namespace and write the main function with an empty body.
A good programming practice is to define all types that shall be used by the function at the beginning of the function body.
In our case, we define a TSequence type for our input sequences and an Align object (TAlign) type to store the alignment.
For more information on the Align datastructure, please read the tutorial Alignment Representation (Gaps).
#include <iostream>
#include <seqan/align.h>
using namespace seqan2;
int main()
{
typedef String<char> TSequence; // sequence type
typedef Align<TSequence, ArrayGaps> TAlign; // align type
After we defined the types, we can define the variables and objects.
First, we create two input sequences seq1 = "CDFGHC" and seq2 = "CDEFGAHC".
We then define an ‘align’ object where we want to put the sequences into, we resize it to manage two Gaps objects, and then assign the sequences to it.
TSequence seq1 = "CDFGHC";
TSequence seq2 = "CDEFGAHC";
TAlign align;
resize(rows(align), 2);
assignSource(row(align, 0), seq1);
assignSource(row(align, 1), seq2);
Now, we can compute our first alignment.
To do so, we simply call the function globalAlignment and give as input parameters the align object and the scoring scheme representing the Levenshtein distance.
The globalAlignment function returns the score of the best alignment, which we store in the score variable.
Afterwards, we print the computed score and the corresponding alignment.
int score = globalAlignment(align, Score<int, Simple>(0, -1, -1));
std::cout << "Score: " << score << std::endl;
std::cout << align << std::endl;
return 0;
}
The output is as follows:
Score: -2
0 .
CD-FG-HC
|| || ||
CDEFGAHC
Assignment 1¶
- Type
Review
Objective
Compute two global alignments between the DNA sequences
"AAATGACGGATTG"."AGTCGGATCTACTG"using the Gotoh algorithm [Got82], implementing the Affine Gap model, with the following scoring parameters:match = 4,mismatch = -2,gapOpen = -4andgapExtend = -2. Store the alignments in two Align objects and print them together with the scores.
- Hints
The Gotoh algorithm uses the Affine Gap function. In SeqAn you can switch between Linear, Affine and Dynamic gap functions by customizing your scoring scheme with one of the three tags
LinearGaps(),AffineGaps()orDynamicGaps()and relative penalty valuesgapOpenandgapExtend. When a single gap value is provided the Linear Gap model is selected as default while the Affine Gap model is chosen as standard when two different gap costs are set. If the Dynamic Gap model [UPA+14] is required the relative tag must be supplied. Have a look on the Scoring Schemes section if you are not sure about the correct ordering.- Solution
First we have to define the body of our program. This includes the definition of the library headers that we want to use. In this case it is the iostream from the STL and the <seqan/align.h> header file defining all algorithms and data structures we want to use. After we added the namespace and opened the main body we define our types we want to use in this function. We use an String with the Dna alphabet, since we know that we work with DNA sequences. The second type is our Align object storing the alignment later on.
#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<Dna> TSequence; // sequence type typedef Align<TSequence, ArrayGaps> TAlign; // align type
In the next step we initialize our objects. This includes the both input sequences
seq1andseq2andalign. We resize the underlying set ofalignthat manages the separate Gaps data structures. Finally, we assign the input sequences as sources to the corresponding row ofalign.TSequence seq1 = "AAATGACGGATTG"; TSequence seq2 = "AGTCGGATCTACTG"; TAlign align; resize(rows(align), 2); assignSource(row(align, 0), seq1); assignSource(row(align, 1), seq2);
Now we compute the alignment using a scoring scheme with affine gap costs. The first parameter corresponds to the
matchvalue, the second to themismatchvalue, the third to thegap extendvalue and the last one to thegap openvalue. We store the computed score of the best alignment in the equally named variablescore. In the end we print the score and the alignment using print methods provided by theiostreammodule of the STL.int score = globalAlignment(align, Score<int, Simple>(4, -2, -2, -4), AffineGaps()); std::cout << "Score: " << score << std::endl; std::cout << align << std::endl; return 0; }
Congratulation! You have computed an alignment using affine gap costs. Here the result of the program:
Score: 16 0 . : . AAATGACGGAT----TG | | ||||| || A---GTCGGATCTACTG
Overlap Alignments¶
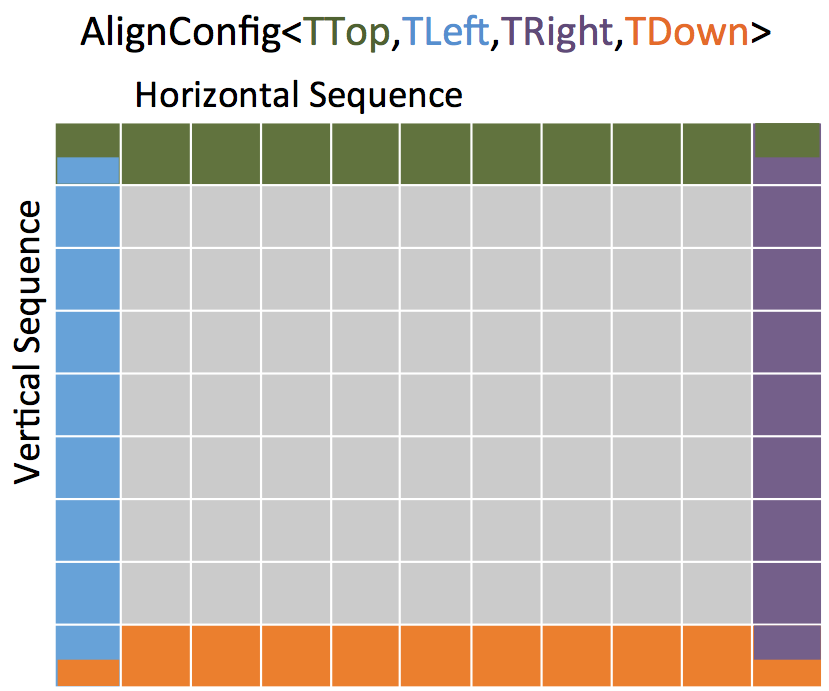
In contrast to the global alignment, an overlap alignment does not penalize gaps at the beginning and at the end of the sequences. This is referred to as free end-gaps. It basically means that overlap alignments can be shifted such that the end of the one sequence matches the beginning of the other sequence, while the respective other ends are gapped.
We use the AlignConfig object to tell the algorithm which gaps are free.
The AlignConfig object takes four explicitly defined bool arguments.
The first argument stands for initial gaps in the vertical sequence of the alignment matrix (first row) and the second argument stands for initial gaps in the horizontal sequence (first column).
The third parameter stands for end gaps in the horizontal sequence (last column) and the fourth parameter stands for end gaps in the vertical sequence (last row).
Per default the arguments of AlignConfig are set to false indicating a standard global alignment as you have seen above.
In an overlap alignment all arguments are set to true.
This means the first row and first column are initialized with zeros and the maximal score is searched in the last column and in the last row.
Just let us compute an overlap alignment to see how it works.
We will also make use of the Alignment Graph to store the alignment this time.
We start again with including the necessary headers and defining all types that we need.
We define the TStringSet type to store our input sequences in a StringSet and we define the TDepStringSet which is an DependentStringSet used internally by the AlignmentGraph.
#include <iostream>
#include <seqan/align.h>
using namespace seqan2;
int main()
{
typedef String<char> TSequence; // sequence type
typedef StringSet<TSequence> TStringSet; // container for strings
typedef StringSet<TSequence, Dependent<> > TDepStringSet; // dependent string set
typedef Graph<Alignment<TDepStringSet> > TAlignGraph; // alignment graph
Before we can initialize the AlignmentGraph we append the input sequences to the StringSet strings.
Then we simply pass strings as an argument to the constructor of the AlignmentGraph alignG.
TSequence seq1 = "blablubalu";
TSequence seq2 = "abba";
TStringSet sequences;
appendValue(sequences, seq1);
appendValue(sequences, seq2);
TAlignGraph alignG(sequences);
Now we are ready to compute the alignment.
This time we change two things when calling the globalAlignment function.
First, we use an AlignmentGraph to store the computed alignment and second we use the AlignConfig object to compute the overlap alignment. The gap model tag can be provided as last argument.
int score = globalAlignment(alignG, Score<int, Simple>(1, -1, -1), AlignConfig<true, true, true, true>(), LinearGaps());
std::cout << "Score: " << score << std::endl;
std::cout << alignG << std::endl;
return 0;
}
The output is as follows.
Score: 2
Alignment matrix:
0 . :
blablubalu
|| ||
--ab--ba--
Assignment 2¶
- Type
Review
- Objective
Compute a semi-global alignment between the sequences
AAATGACGGATTGandTGGGAusing the costs 1, -1, -1 for match, mismatch and gap, respectively. Use an AlignmentGraph to store the alignment. Print the score and the resulting alignment to the standard output.- Hint
A semi-global alignment is a special form of an overlap alignment often used when aligning short sequences against a long sequence. Here we only allow free end-gaps at the beginning and the end of the shorter sequence.
- Solution
First we have to define the body of our program. This includes the definition of the library headers that we want to use. In this case we include the
iostreamheader from the STL and the<seqan/align.h>header, which defines all algorithms and data structures we want to use. After we added the namespace and opened themainfunction body we define our types we want to use in this function. We use an String with the Dna alphabet, since we know that we work with DNA sequences. We use an additional StringSet to store the input sequences. In this scenario we use an AlignmentGraph to store the alignment. Remember, that the AlignmentGraph uses an DependentStringSet to map the vertices to the correct input sequences.#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<Dna> TSequence; // sequence type typedef StringSet<TSequence> TStringSet; // container for strings typedef StringSet<TSequence, Dependent<> > TDepStringSet; // dependent string set typedef Graph<Alignment<TDepStringSet> > TAlignGraph; // alignment graph
In the next step we initialize our input StringSet
stringsand pass it as argument to the constructor of the AlignmentGraphalignG.TSequence seq1 = "AAATGACGGATTG"; TSequence seq2 = "TGGGA"; TStringSet sequences; appendValue(sequences, seq1); appendValue(sequences, seq2); TAlignGraph alignG(sequences);
Now we compute the alignment using the Levenshtein distance and a AlignConfig object to set the correct free end-gaps. In this example we put the shorter sequence on the vertical axis of our alignment matrix. Hence, we have to use free end-gaps in the first and last row, which corresponds to the first and the last parameter in the AlignConfig object. If you add the shorter sequence at first to
strings, then you simply have to flip theboolvalues of the AlignConfig object.int score = globalAlignment(alignG, Score<int, Simple>(1, -1, -1), AlignConfig<true, false, false, true>()); std::cout << "Score: " << score << std::endl; std::cout << alignG << std::endl; return 0; }
Here the result of the program.
Score: 3 Alignment matrix: 0 . : AAATGACGGATTG || ||| ---TG--GGA---
Specialized Alignments¶
SeqAn offers specialized algorithms that can be selected using a tag. Note that often these specializations are restricted in some manner. The following list shows different alignment tags for specialized alignment algorithms and the restrictions of the algorithms.
- Hirschberg
The Hirschberg algorithm computes an alignment between two sequences in linear space. The algorithm can only be used with an Align object (or Gaps). It uses only linear gap costs and does no overlap alignments.
- MyersBitVector
The MyersBitVector is a fast alignment specialization using bit parallelism. It only works with the Levenshtein distance and outputs no alignments.
- MyersHirschberg
The MyersHirschberg is an combination of the rapid MyersBitVector and the space efficient Hirschberg algorithm, which additionally enables the computation of an alignment. It only works with the Levenshtein distance and for Align objects.
Tip
In SeqAn you can omit the computation of the traceback to get only the score by using the function globalAlignmentScore. This way you can use the alignment algorithms for verification purposes, etc.
In the following example, we want to compute a global alignment of two sequences using the Hirschberg algorithm.
We are setting the match score to 1, and mismatch as well as gap penalty to -1.
We print the alignment and the score.
First the necessary includes and typedefs:
#include <iostream>
#include <seqan/align.h>
using namespace seqan2;
int main()
{
typedef String<char> TSequence; // sequence type
typedef Align<TSequence, ArrayGaps> TAlign; // align type
TSequence seq1 = "GARFIELDTHECAT";
TSequence seq2 = "GARFIELDTHEBIGCAT";
TAlign align;
resize(rows(align), 2);
assignSource(row(align, 0), seq1);
assignSource(row(align, 1), seq2);
In addition to the previous examined examples we tell the globalAlignment function to use the desired Hirschberg algorithm by explicitly passing the tag Hirschberg as last parameter.
The resulting alignment and score are then printed.
int score = globalAlignment(align, Score<int, Simple>(1, -1, -1), Hirschberg());
std::cout << "Score: " << score << std::endl;
std::cout << align << std::endl;
return 0;
}
The output is as follows.
Score: 11
0 . : .
GARFIELDTHE---CAT
||||||||||| |||
GARFIELDTHEBIGCAT
Assignment 3¶
- Type
Application
- Objective
Write a program that computes a global alignment between the Rna sequences
AAGUGACUUAUUGandAGUCGGAUCUACUGusing the Myers-Hirschberg variant. You should use the Align data structure to store the alignment. Print the score and the alignment. Additionally, output for each row of the Align object the view positions of the gaps.- Hint
You can use an iterator to iterate over a row. Use the metafunction Row to get the type of the row used by the Align object. Use the function isGap to check whether the current value of the iterator is a gap or not. The gaps are already in the view space.
- Solution
As usual, first the necessary includes and typedefs. Our sequence type is
String<Rna>.TAlignandTRoware defined as in the previous example program. The typeIterator<TRow>::Typewill be used to iterate over the rows of the alignment.#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<Rna> TSequence; typedef Align<TSequence, ArrayGaps> TAlign; typedef Row<TAlign>::Type TRow; typedef Iterator<TRow>::Type TRowIterator;
In the next step we initialize our Align object
alignwith the corresponding source files.TSequence seq1 = "AAGUGACUUAUUG"; TSequence seq2 = "AGUCGGAUCUACUG"; TAlign align; resize(rows(align), 2); assignSource(row(align, 0), seq1); assignSource(row(align, 1), seq2);
Now we compute the alignment using Myers-Hirschberg algorithm by specifying the correct tag at the end of the function.
int score = globalAlignment(align, MyersHirschberg()); std::cout << "Score: " << score << std::endl; std::cout << align << std::endl;
Finally, we iterate over both gap structures and print the view positions of the gaps within the sequences.
unsigned aliLength = _max(length(row(align, 0)), length(row(align, 1))); for (unsigned i = 0; i < length(rows(align)); ++i) { TRowIterator it = iter(row(align, i), 0); TRowIterator itEnd = iter(row(align, i), aliLength); unsigned pos = 0; std::cout << "Row " << i << " contains gaps at positions: "; std::cout << std::endl; while (it != itEnd) { if (isGap(it)) std::cout << pos << std::endl; ++it; ++pos; } } return 0; }
The output of the program is as follows.
Score: -6 0 . : . AAGU--GA-CUUAUUG | || || || | || A-GUCGGAUCU-ACUG Row 0 contains gaps at positions: 4 5 8 Row 1 contains gaps at positions: 1 11
Local Alignments¶
Now let’s look at local pairwise alignments.
SeqAn offers the classical Smith-Waterman algorithm that computes the best local alignment with respect to a given scoring scheme, and the Waterman-Eggert algorithm, which computes not only the best but also suboptimal local alignments.
We are going to demonstrate the usage of both in the following example where first the best local alignment of two character strings and then all local alignments of two DNA sequences with a score greater than or equal to 4 are computed.
#include <iostream>
#include <seqan/align.h>
using namespace seqan2;
int main()
{
Let’s start with initializing the Align object to contain the two sequences.
Align<String<char> > ali;
resize(rows(ali), 2);
assignSource(row(ali, 0), "aphilologicaltheorem");
assignSource(row(ali, 1), "bizarreamphibology");
Now the best alignment given the scoring parameters is computed using the Dynamic Gap model by the function localAlignment. The returned score value is printed directly, and the alignment itself in the next line. The functions clippedBeginPosition and clippedEndPosition can be used to retrieve the begin and end position of the matching subsequences within the original sequences.
std::cout << "Score = " << localAlignment(ali, Score<int>(3, -3, -2, -2), DynamicGaps()) << std::endl;
std::cout << ali;
std::cout << "Aligns Seq1[" << clippedBeginPosition(row(ali, 0)) << ":" << (clippedEndPosition(row(ali, 0)) - 1) << "]";
std::cout << " and Seq2[" << clippedBeginPosition(row(ali, 1)) << ":" << (clippedEndPosition(row(ali, 1)) - 1) << "]" << std::endl << std::endl;
Next, several local alignments of the two given DNA sequences are going to be computed. First, the Align object is created.
Align<String<Dna> > ali2;
resize(rows(ali2), 2);
assignSource(row(ali2, 0), "ataagcgtctcg");
assignSource(row(ali2, 1), "tcatagagttgc");
A LocalAlignmentEnumerator object needs to be initialized on the Align object.
In addition to the Align object and the scoring scheme, we now also pass the finder and a minimal score value, 4 in this case, to the localAlignment function.
The WatermanEggert tag specifies the desired Waterman-Eggert algorithm.
While the score of the local alignment satisfies the minimal score cutoff, the alignments are printed with their scores and the subsequence begin and end positions.
Score<int> scoring(2, -1, -2, 0);
LocalAlignmentEnumerator<Score<int>, Unbanded> enumerator(scoring, 5);
while (nextLocalAlignment(ali2, enumerator))
{
std::cout << "Score = " << getScore(enumerator) << std::endl;
std::cout << ali2;
std::cout << "Aligns Seq1[" << clippedBeginPosition(row(ali2, 0)) << ":" << (clippedEndPosition(row(ali2, 0)) - 1) << "]";
std::cout << " and Seq2[" << clippedBeginPosition(row(ali2, 1)) << ":" << (clippedEndPosition(row(ali2, 1)) - 1) << "]" << std::endl << std::endl;
}
return 0;
}
Here is the output of our example program. The first part outputs one alignment. The second part outputs two alignments:
Score = 19
0 . :
a-philolog
| ||| ||||
amphibolog
Aligns Seq1[0:9] and Seq2[7:16]
Score = 9
0 .
ATAAGCGT
||| | ||
ATA-GAGT
Aligns Seq1[0:7] and Seq2[2:9]
Score = 5
0 .
TC-TCG
|| | |
TCATAG
Aligns Seq1[7:12] and Seq2[0:5]
Assignment 4¶
- Type
Review
- Objective
Write a program which computes the 3 best local alignments of the two AminoAcid sequences “
PNCFDAKQRTASRPL” and “CFDKQKNNRTATRDTA” using the following scoring parameters:match = 3,mismatch = -2,gap open = -5,gap extension = -1.- Hint
Use an extra variable to enumerate the k best alignments.
- Solution
The usual includes.
#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() {
The initialization of the Align object.
Align<String<AminoAcid> > ali; resize(rows(ali), 2); assignSource(row(ali, 0), "PNCFDAKQRTASRPL"); assignSource(row(ali, 1), "CFDKQKNNRTATRDTA");
Computing the three best alignments with the desired scoring parameters:
Score<int> sc(3, -2, -1, -5); unsigned count = 0; LocalAlignmentEnumerator<Score<int>, Unbanded> enumerator(sc); while (nextLocalAlignment(ali, enumerator) && count < 3) { std::cout << "Score = " << getScore(enumerator) << std::endl; std::cout << ali; ++count; } return 0; }
The resulting output is as follows.
Score = 21 0 . : CFDAKQ---RTASR ||| || ||| | CFD-KQKNNRTATR Score = 8 0 . AKQR-TA | | || AT-RDTA Score = 5 0 D-A | | DTA
Banded Alignments¶
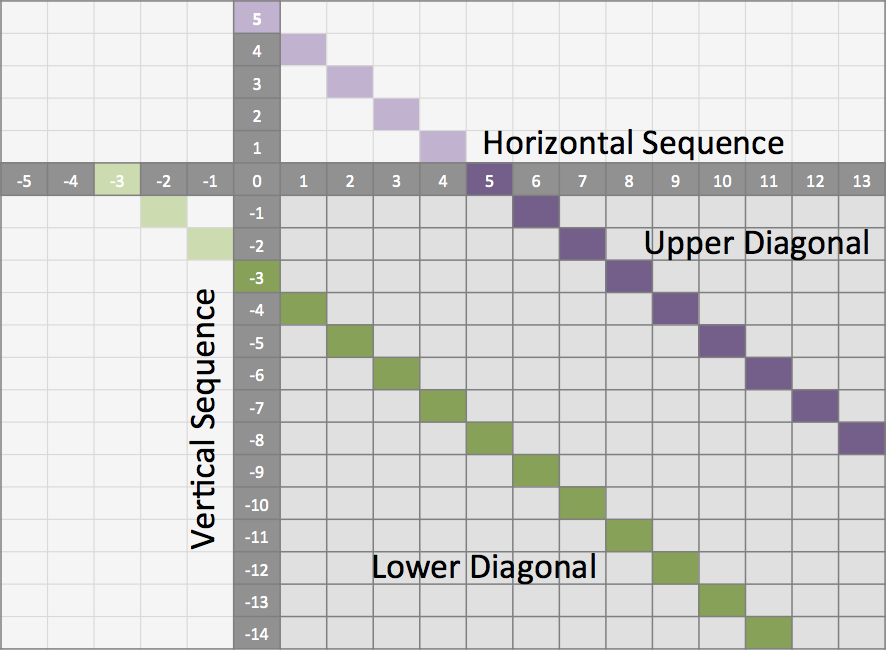
Often it is quite useful to reduce the search space in which the optimal alignment can be found, e.g., if the sequences are very similar, or if only a certain number of errors is allowed.
To do so you can define a band, whose intersection with the alignment matrix defines the search space.
To define a band we have to pass two additional parameters to the alignment function.
The first one specifies the position where the lower diagonal of the band crosses the vertical axis.
The second one specifies the position where the upper diagonal of the band crosses the horizontal axis.
You can imagine the matrix as the fourth quadrant of the Cartesian coordinate system.
Then the main diagonal of an alignment matrix is described by the function f(x) = -x, all diagonals that crosses the vertical axis below this point are specified with negative values while all diagonals that crosses the horizontal axis are specified with positive values (see image).
A given band is valid as long as the relation lower diagonal <= upper diagonal holds.
In case of equality, the alignment is equivalent to the hamming distance problem, where only substitutions are considered.
Important
The alignment algorithms return MinValue<ScoreValue>::VALUE if a correct alignment cannot be computed due to invalid compositions of the band and the specified alignment preferences.
Assume, you compute a global alignment and the given band does not cover the last cell of the alignment matrix.
In this case it is not possible to compute a correct alignment, hence MinValue<ScoreValue>::VALUE is returned, while no further alignment information are computed.
Let’s compute a banded alignment.
The first step is to write the main function body including the type definitions and the initializations.
#include <iostream>
#include <seqan/align.h>
using namespace seqan2;
int main()
{
typedef String<char> TSequence; // sequence type
typedef Align<TSequence, ArrayGaps> TAlign; // align type
TSequence seq1 = "CDFGHC";
TSequence seq2 = "CDEFGAHC";
TAlign align;
resize(rows(align), 2);
assignSource(row(align, 0), seq1);
assignSource(row(align, 1), seq2);
After we initialized everything, we will compute the banded alignment.
We pass the values -2 for the lower diagonal and 2 for the upper diagonal.
int score = globalAlignment(align, Score<int, Simple>(0, -1, -1), -2, 2);
std::cout << "Score: " << score << std::endl;
std::cout << align << std::endl;
return 0;
}
And here is the output:
Score: -2
0 .
CD-FG-HC
|| || ||
CDEFGAHC
Assignment 5¶
- Type
Transfer
- Objective
Write an approximate pattern matching algorithm using alignment algorithms. Report the positions of all hits where the pattern matches the text with at most
2errors. Output the number of total edits used to match the pattern and print the corresponding cigar string of the alignment without leading and trailing gaps in the pattern. Text: “MISSISSIPPIANDMISSOURI” Pattern: “SISSI”- Hint
The first step would be to verify at which positions in the text the pattern matches with at most 2 errors.
Use the infix function to return a subsequence of a string.
A CIGAR string is a different representation of an alignment. It consists of a number followed by an operation. The number indicates how many operations are executed. Operations can be M for match or mismatch, I for insertion and D for deletion. Here is an example:
ref: AC--GTCATTT r01: ACGTCTCA--- Cigar of r01: 2M2I4M3D
- Solution (Step 1)
#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<char> TSequence; TSequence text = "MISSISSIPPIANDMISSOURI"; TSequence pattern = "SISSI"; String<int> locations; for (unsigned i = 0; i < length(text) - length(pattern); ++i) { // Compute the MyersBitVector in current window of text. TSequence tmp = infix(text, i, i + length(pattern)); // Report hits with at most 2 errors. if (globalAlignmentScore(tmp, pattern, MyersBitVector()) >= -2) { appendValue(locations, i); } } return 0; }
- Solution (Step 2)
#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<char> TSequence; typedef Gaps<TSequence, ArrayGaps> TGaps; typedef Iterator<String<int> >::Type TIterator; TSequence text = "MISSISSIPPIANDMISSOURI"; TSequence pattern = "SISSI"; String<int> locations; for (unsigned i = 0; i < length(text) - length(pattern); ++i) { // Compute the MyersBitVector in current window of text. TSequence tmp = infix(text, i, i + length(pattern)); // Report hits with at most 2 errors. if (globalAlignmentScore(tmp, pattern, MyersBitVector()) >= -2) { appendValue(locations, i); } } TGaps gapsText; TGaps gapsPattern; assignSource(gapsPattern, pattern); std::cout << "Text: " << text << "\tPattern: " << pattern << std::endl; for (TIterator it = begin(locations); it != end(locations); ++it) { // Clear previously computed gaps. clearGaps(gapsText); clearGaps(gapsPattern); // Only recompute the area within the current window over the text. TSequence textInfix = infix(text, *it, *it + length(pattern)); assignSource(gapsText, textInfix); // Use semi-global alignment since we do not want to track leading/trailing gaps in the pattern. // Restirct search space using a band allowing at most 2 errors in vertical/horizontal direction. int score = globalAlignment(gapsText, gapsPattern, Score<int>(0, -1, -1), AlignConfig<true, false, false, true>(), -2, 2); std::cout << "Hit at position " << *it << "\ttotal edits: " << abs(score) << std::endl; } return 0; }
- Solution (Step 3)
#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<char> TSequence; typedef Gaps<TSequence, ArrayGaps> TGaps; typedef Iterator<TGaps>::Type TGapsIterator; typedef Iterator<String<int> >::Type TIterator; TSequence text = "MISSISSIPPIANDMISSOURI"; TSequence pattern = "SISSI"; String<int> locations; for (unsigned i = 0; i < length(text) - length(pattern); ++i) { // Compute the MyersBitVector in current window of text. TSequence tmp = infix(text, i, i + length(pattern)); // Report hits with at most 2 errors. if (globalAlignmentScore(tmp, pattern, MyersBitVector()) >= -2) { appendValue(locations, i); } } TGaps gapsText; TGaps gapsPattern; assignSource(gapsPattern, pattern); std::cout << "Text: " << text << "\tPattern: " << pattern << std::endl; for (TIterator it = begin(locations); it != end(locations); ++it) { // Clear previously computed gaps. clearGaps(gapsText); clearGaps(gapsPattern); // Only recompute the area within the current window over the text. TSequence textInfix = infix(text, *it, *it + length(pattern)); assignSource(gapsText, textInfix); // Use semi-global alignment since we do not want to track leading/trailing gaps in the pattern. // Restirct search space using a band allowing at most 2 errors in vertical/horizontal direction. int score = globalAlignment(gapsText, gapsPattern, Score<int>(0, -1, -1), AlignConfig<true, false, false, true>(), -2, 2); TGapsIterator itGapsPattern = begin(gapsPattern); TGapsIterator itGapsEnd = end(gapsPattern); // Remove trailing gaps in pattern. int count = 0; while (isGap(--itGapsEnd)) ++count; setClippedEndPosition(gapsPattern, length(gapsPattern) - count); // Remove leading gaps in pattern. if (isGap(itGapsPattern)) { setClippedBeginPosition(gapsPattern, countGaps(itGapsPattern)); setClippedBeginPosition(gapsText, countGaps(itGapsPattern)); } std::cout << "Hit at position " << *it << "\ttotal edits: " << abs(score) << std::endl; } return 0; }
- Solution (Step 4)
#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<char> TSequence; typedef Gaps<TSequence, ArrayGaps> TGaps; typedef Iterator<TGaps>::Type TGapsIterator; typedef Iterator<String<int> >::Type TIterator; TSequence text = "MISSISSIPPIANDMISSOURI"; TSequence pattern = "SISSI"; String<int> locations; for (unsigned i = 0; i < length(text) - length(pattern); ++i) { // Compute the MyersBitVector in current window of text. TSequence tmp = infix(text, i, i + length(pattern)); // Report hits with at most 2 errors. if (globalAlignmentScore(tmp, pattern, MyersBitVector()) >= -2) { appendValue(locations, i); } } TGaps gapsText; TGaps gapsPattern; assignSource(gapsPattern, pattern); std::cout << "Text: " << text << "\tPattern: " << pattern << std::endl; for (TIterator it = begin(locations); it != end(locations); ++it) { // Clear previously computed gaps. clearGaps(gapsText); clearGaps(gapsPattern); // Only recompute the area within the current window over the text. TSequence textInfix = infix(text, *it, *it + length(pattern)); assignSource(gapsText, textInfix); // Use semi-global alignment since we do not want to track leading/trailing gaps in the pattern. // Restirct search space using a band allowing at most 2 errors in vertical/horizontal direction. int score = globalAlignment(gapsText, gapsPattern, Score<int>(0, -1, -1), AlignConfig<true, false, false, true>(), -2, 2); TGapsIterator itGapsPattern = begin(gapsPattern); TGapsIterator itGapsEnd = end(gapsPattern); // Remove trailing gaps in pattern. int count = 0; while (isGap(--itGapsEnd)) ++count; setClippedEndPosition(gapsPattern, length(gapsPattern) - count); // Remove leading gaps in pattern. if (isGap(itGapsPattern)) { setClippedBeginPosition(gapsPattern, countGaps(itGapsPattern)); setClippedBeginPosition(gapsText, countGaps(itGapsPattern)); } // Reinitilaize the iterators. TGapsIterator itGapsText = begin(gapsText); itGapsPattern = begin(gapsPattern); itGapsEnd = end(gapsPattern); // Use a stringstream to construct the cigar string. std::stringstream cigar; while (itGapsPattern != itGapsEnd) { // Count insertions. if (isGap(itGapsText)) { int numGaps = countGaps(itGapsText); cigar << numGaps << "I"; itGapsText += numGaps; itGapsPattern += numGaps; continue; } ++itGapsText; ++itGapsPattern; } std::cout << "Hit at position " << *it << "\ttotal edits: " << abs(score) << std::endl; } return 0; }
- Solution (Step 5)
#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<char> TSequence; typedef Gaps<TSequence, ArrayGaps> TGaps; typedef Iterator<TGaps>::Type TGapsIterator; typedef Iterator<String<int> >::Type TIterator; TSequence text = "MISSISSIPPIANDMISSOURI"; TSequence pattern = "SISSI"; String<int> locations; for (unsigned i = 0; i < length(text) - length(pattern); ++i) { // Compute the MyersBitVector in current window of text. TSequence tmp = infix(text, i, i + length(pattern)); // Report hits with at most 2 errors. if (globalAlignmentScore(tmp, pattern, MyersBitVector()) >= -2) { appendValue(locations, i); } } TGaps gapsText; TGaps gapsPattern; assignSource(gapsPattern, pattern); std::cout << "Text: " << text << "\tPattern: " << pattern << std::endl; for (TIterator it = begin(locations); it != end(locations); ++it) { // Clear previously computed gaps. clearGaps(gapsText); clearGaps(gapsPattern); // Only recompute the area within the current window over the text. TSequence textInfix = infix(text, *it, *it + length(pattern)); assignSource(gapsText, textInfix); // Use semi-global alignment since we do not want to track leading/trailing gaps in the pattern. // Restirct search space using a band allowing at most 2 errors in vertical/horizontal direction. int score = globalAlignment(gapsText, gapsPattern, Score<int>(0, -1, -1), AlignConfig<true, false, false, true>(), -2, 2); TGapsIterator itGapsPattern = begin(gapsPattern); TGapsIterator itGapsEnd = end(gapsPattern); // Remove trailing gaps in pattern. int count = 0; while (isGap(--itGapsEnd)) ++count; setClippedEndPosition(gapsPattern, length(gapsPattern) - count); // Remove leading gaps in pattern. if (isGap(itGapsPattern)) { setClippedBeginPosition(gapsPattern, countGaps(itGapsPattern)); setClippedBeginPosition(gapsText, countGaps(itGapsPattern)); } // Reinitilaize the iterators. TGapsIterator itGapsText = begin(gapsText); itGapsPattern = begin(gapsPattern); itGapsEnd = end(gapsPattern); // Use a stringstream to construct the cigar string. std::stringstream cigar; while (itGapsPattern != itGapsEnd) { // Count insertions. if (isGap(itGapsText)) { int numGaps = countGaps(itGapsText); cigar << numGaps << "I"; itGapsText += numGaps; itGapsPattern += numGaps; continue; } // Count deletions. if (isGap(itGapsPattern)) { int numGaps = countGaps(itGapsPattern); cigar << numGaps << "D"; itGapsText += numGaps; itGapsPattern += numGaps; continue; } ++itGapsText; ++itGapsPattern; } // Output the hit position in the text, the total number of edits and the corresponding cigar string. std::cout << "Hit at position " << *it << "\ttotal edits: " << abs(score) << std::endl; } return 0; }
- Solution (Step 6)
#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<char> TSequence; typedef Gaps<TSequence, ArrayGaps> TGaps; typedef Iterator<TGaps>::Type TGapsIterator; typedef Iterator<String<int> >::Type TIterator; TSequence text = "MISSISSIPPIANDMISSOURI"; TSequence pattern = "SISSI"; String<int> locations; for (unsigned i = 0; i < length(text) - length(pattern); ++i) { // Compute the MyersBitVector in current window of text. TSequence tmp = infix(text, i, i + length(pattern)); // Report hits with at most 2 errors. if (globalAlignmentScore(tmp, pattern, MyersBitVector()) >= -2) { appendValue(locations, i); } } TGaps gapsText; TGaps gapsPattern; assignSource(gapsPattern, pattern); std::cout << "Text: " << text << "\tPattern: " << pattern << std::endl; for (TIterator it = begin(locations); it != end(locations); ++it) { // Clear previously computed gaps. clearGaps(gapsText); clearGaps(gapsPattern); // Only recompute the area within the current window over the text. TSequence textInfix = infix(text, *it, *it + length(pattern)); assignSource(gapsText, textInfix); // Use semi-global alignment since we do not want to track leading/trailing gaps in the pattern. // Restirct search space using a band allowing at most 2 errors in vertical/horizontal direction. int score = globalAlignment(gapsText, gapsPattern, Score<int>(0, -1, -1), AlignConfig<true, false, false, true>(), -2, 2); TGapsIterator itGapsPattern = begin(gapsPattern); TGapsIterator itGapsEnd = end(gapsPattern); // Remove trailing gaps in pattern. int count = 0; while (isGap(--itGapsEnd)) ++count; setClippedEndPosition(gapsPattern, length(gapsPattern) - count); // Remove leading gaps in pattern. if (isGap(itGapsPattern)) { setClippedBeginPosition(gapsPattern, countGaps(itGapsPattern)); setClippedBeginPosition(gapsText, countGaps(itGapsPattern)); } // Reinitilaize the iterators. TGapsIterator itGapsText = begin(gapsText); itGapsPattern = begin(gapsPattern); itGapsEnd = end(gapsPattern); // Use a stringstream to construct the cigar string. std::stringstream cigar; int numMatchAndMismatches = 0; while (itGapsPattern != itGapsEnd) { // Count insertions. if (isGap(itGapsText)) { int numGaps = countGaps(itGapsText); cigar << numGaps << "I"; itGapsText += numGaps; itGapsPattern += numGaps; continue; } // Count deletions. if (isGap(itGapsPattern)) { int numGaps = countGaps(itGapsPattern); cigar << numGaps << "D"; itGapsText += numGaps; itGapsPattern += numGaps; continue; } // Count matches and mismatches. while (itGapsPattern != itGapsEnd) { if (isGap(itGapsPattern) || isGap(itGapsText)) break; ++numMatchAndMismatches; ++itGapsText; ++itGapsPattern; } if (numMatchAndMismatches != 0) cigar << numMatchAndMismatches << "M"; numMatchAndMismatches = 0; } // Output the hit position in the text, the total number of edits and the corresponding cigar string. std::cout << "Hit at position " << *it << "\ttotal edits: " << abs(score) << "\tcigar: " << cigar.str() << std::endl; } return 0; }
- Complete Solution (and more explanations)
Write the main body of the program with type definition and initialization of the used data structures.
#include <iostream> #include <seqan/align.h> using namespace seqan2; int main() { typedef String<char> TSequence; typedef Gaps<TSequence, ArrayGaps> TGaps; typedef Iterator<TGaps>::Type TGapsIterator; typedef Iterator<String<int> >::Type TIterator; TSequence text = "MISSISSIPPIANDMISSOURI"; TSequence pattern = "SISSI";
In the first part of the algorithm we implement an alignment based verification process to identify positions in the subject sequence at which we can find our pattern with at most 2 errors. We slide the 5*5 alignment matrix position by position over the subject sequence and use the MeyersBitVector to verify the hits. If the score is greater or equal than -2, then we have found a hit. We store the begin position of the hit in locations.
String<int> locations; for (unsigned i = 0; i < length(text) - length(pattern); ++i) { // Compute the MyersBitVector in current window of text. TSequence tmp = infix(text, i, i + length(pattern)); // Report hits with at most 2 errors. if (globalAlignmentScore(tmp, pattern, MyersBitVector()) >= -2) { appendValue(locations, i); } }
In the second part of the algorithm we iterate over all reported locations. This time we compute a semi-global alignment since we won’t penalize gaps at the beginning and at the end of our pattern. We also compute a band allowing at most 2 errors in either direction. Don’t forget to clear the gaps in each iteration, otherwise we might encounter wrong alignments.
TGaps gapsText; TGaps gapsPattern; assignSource(gapsPattern, pattern); std::cout << "Text: " << text << "\tPattern: " << pattern << std::endl; for (TIterator it = begin(locations); it != end(locations); ++it) { // Clear previously computed gaps. clearGaps(gapsText); clearGaps(gapsPattern); // Only recompute the area within the current window over the text. TSequence textInfix = infix(text, *it, *it + length(pattern)); assignSource(gapsText, textInfix); // Use semi-global alignment since we do not want to track leading/trailing gaps in the pattern. // Restirct search space using a band allowing at most 2 errors in vertical/horizontal direction. int score = globalAlignment(gapsText, gapsPattern, Score<int>(0, -1, -1), AlignConfig<true, false, false, true>(), -2, 2);
In the next part we determine the cigar string for the matched pattern. We have to remove leading and trailing gaps in the gapsPattern object using the functions setClippedBeginPosition and setClippedEndPosition. We also need to set the clipped begin position for the gapsText object such that both Gaps begin at the same position.
TGapsIterator itGapsPattern = begin(gapsPattern); TGapsIterator itGapsEnd = end(gapsPattern); // Remove trailing gaps in pattern. int count = 0; while (isGap(--itGapsEnd)) ++count; setClippedEndPosition(gapsPattern, length(gapsPattern) - count); // Remove leading gaps in pattern. if (isGap(itGapsPattern)) { setClippedBeginPosition(gapsPattern, countGaps(itGapsPattern)); setClippedBeginPosition(gapsText, countGaps(itGapsPattern)); } // Reinitilaize the iterators. TGapsIterator itGapsText = begin(gapsText); itGapsPattern = begin(gapsPattern); itGapsEnd = end(gapsPattern); // Use a stringstream to construct the cigar string. std::stringstream cigar; int numMatchAndMismatches = 0; while (itGapsPattern != itGapsEnd) {
First, we identify insertions using the functions isGap and countGaps.
// Count insertions. if (isGap(itGapsText)) { int numGaps = countGaps(itGapsText); cigar << numGaps << "I"; itGapsText += numGaps; itGapsPattern += numGaps; continue; }
We do the same to identify deletions.
// Count deletions. if (isGap(itGapsPattern)) { int numGaps = countGaps(itGapsPattern); cigar << numGaps << "D"; itGapsText += numGaps; itGapsPattern += numGaps; continue; }
If there is neither an insertion nor a deletion, then there must be a match or a mismatch. As long as we encounter matches and mismatches we move forward in the Gaps structures. Finally we print out the position of the hit, its total number of edits and the corresponding cigar string.
// Count matches and mismatches. while (itGapsPattern != itGapsEnd) { if (isGap(itGapsPattern) || isGap(itGapsText)) break; ++numMatchAndMismatches; ++itGapsText; ++itGapsPattern; } if (numMatchAndMismatches != 0) cigar << numMatchAndMismatches << "M"; numMatchAndMismatches = 0; } // Output the hit position in the text, the total number of edits and the corresponding cigar string. std::cout << "Hit at position " << *it << "\ttotal edits: " << abs(score) << "\tcigar: " << cigar.str() << std::endl; } return 0; }
Here is the output of this program.
Text: MISSISSIPPIANDMISSOURI Pattern: SISSI Hit at position 0 total edits: 1 cigar: 5M Hit at position 1 total edits: 1 cigar: 1I4M Hit at position 2 total edits: 1 cigar: 4M1I Hit at position 3 total edits: 0 cigar: 5M Hit at position 4 total edits: 1 cigar: 1I4M Hit at position 6 total edits: 2 cigar: 5M Hit at position 14 total edits: 2 cigar: 4M1I