Suffix Tree¶
We consider an alphabet Σ and a sentinel character $ that is smaller than every character of Σ. A suffix tree of a given non-empty string s over Σ is a directed tree whose edges are labeled with non-empty substrings of s$ with the following properties:
- Each outgoing edge begins with a different letter and the outdegree of an internal node is greater than 1.
- Each suffix of s$ is the concatenation of edges from the root to a leaf node.
- Each path from the root to a leaf node is a suffix of s$.
The following figure shows the suffix tree of the string s=”mississippi” (suffix nodes are shaded):
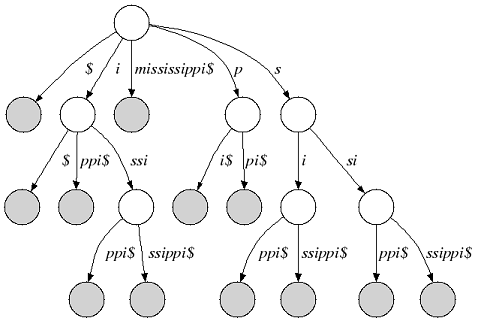
Figure 1: Suffix tree of “mississippi”
Many suffix tree construction algorithms expect $ to be part of the string alphabet which is undesirable for small bit-compressible alphabets (e.g. DNA). In SeqAn there is no need to introduce a $. We relax suffix tree criterion 2. and consider the relaxed suffix tree that arises from the suffix tree of s by removing the $ character and all empty edges. In the following, we only consider relaxed suffix trees and simply call them suffix trees. In that tree a suffix can end in an inner node as you can see in the next figure (suffix “i”):
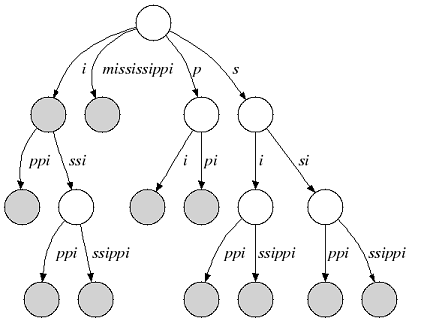
Figure 2: Relaxed suffix tree of “mississippi”