Graphs¶
- Learning Objective
- This tutorial shows how to use graphs in SeqAn and their functionality.
- Difficulty
- Average
- Duration
- 1 h
- Prerequisites
- Sequences, Alignment Representation, Pairwise Sequence Alignment
A graph in computer science is an ordered pair \(G = (V, E)\) of a set of vertices V and a set of edges E. SeqAn provides different Graph types of graphs and the most well-known graph algorithms as well as some specialized alignment graph algorithms. In this part of the tutorial, we demonstrate how to construct a graph in SeqAn and show the usage of some algorithms. Alignment graphs are described in the tutorial Alignment Representation.
Let us follow a simple example. We have given the following network of five cities and in this network we want to compute the shortest path from Hannover to any other city.
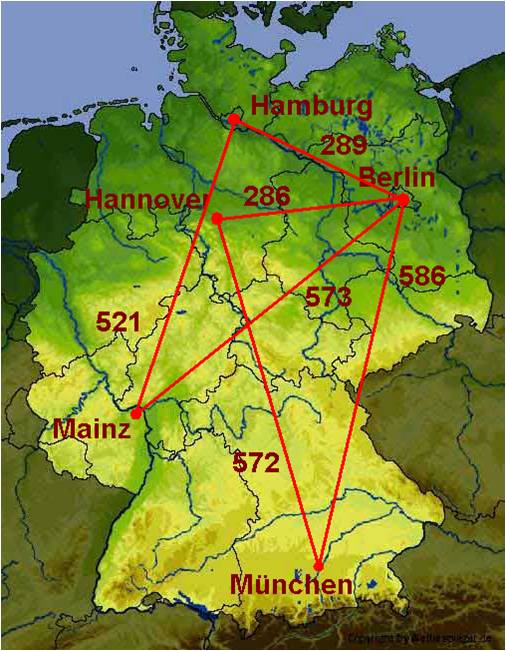
In the section Graph Basics, we will create the network and write the graph to a .dot file. The section Property Maps and Iterators assigns city names to the vertices and demonstrates the usage of a vertex iterator. Finally, in Graph Algorithms we will compute the shortest path by calling a single function.
After having worked through these sections you should be familiar with the general usage of graphs in SeqAn.
Graph Basics¶
The general header file for all types of graphs is <seqan/graph_types.h>. It comprises the class Graph and its specializations, all functions for basic graph operations, and different iterators. Later, for computing the shortest path we will also need <seqan/graph_algorithms.h> which includes the implementations of most of SeqAn’s graph algorithms.
#include <iostream>
#include <seqan/graph_types.h>
#include <seqan/graph_algorithms.h>
using namespace seqan;
We want to model the network of cities as an undirected graph and label the edges with distances. Before we start creating edges and vertices, we need some typedefs to specify the graph type.
SeqAn offers different specializations of the class Graph:, Undirected Graph, DirectedGraph, Tree, Automaton, HmmGraph, and Alignment Graph. For our example, an undirected graph will be sufficient, so we define our own graph type TGraph with the specialization Undirected Graph of the class Graph. Luckily, this specialization has an optional cargo template argument, which attaches any kind of object to the edges of the graph. This enables us to store the distances between the cities, our edge labels, using the cargo type TCargo defined as unsigned int. Using the cargo argument, we have to provide a distance when adding an edge. And when we remove an edge we also remove the distance.
int main ()
{
typedef unsigned int TCargo;
typedef Graph<Undirected<TCargo> > TGraph;
typedef VertexDescriptor<TGraph>::Type TVertexDescriptor;
Each vertex and each edge in a graph is identified by a so-called descriptor. The type of the descriptors is returned by the metafunction VertexDescriptor. In our example, we define a type TVertexDescriptor by calling VertexDescriptor on our graph type. Analogously, there is the metafunction EdgeDescriptor for edge descriptors.
We can now create the graph g of our type TGraph.
TGraph g;
For our example, we add five vertices for the five cities, and six edges connecting the cities.
Vertices can be added to g by a call to the function addVertex. The function returns the descriptor of the created vertex. These descriptors are needed to add the edges afterwards.
TVertexDescriptor vertBerlin = addVertex(g);
TVertexDescriptor vertHamburg = addVertex(g);
TVertexDescriptor vertHannover = addVertex(g);
TVertexDescriptor vertMainz = addVertex(g);
TVertexDescriptor vertMuenchen = addVertex(g);
The function addEdge adds an edge to the graph. The arguments of this function are the graph to which the edge is added, the vertices that it connects, and the cargo (which is in our case the distance between the two cities).
addEdge(g, vertBerlin, vertHamburg, 289);
addEdge(g, vertBerlin, vertHannover, 286);
addEdge(g, vertBerlin, vertMainz, 573);
addEdge(g, vertBerlin, vertMuenchen, 586);
addEdge(g, vertHannover, vertMuenchen, 572);
addEdge(g, vertHamburg, vertMainz, 521);
Once we have created the graph we may want to have a look at it. SeqAn offers the possibility to write a graph to a dot file. With a tool like Graphviz you can then visualize the graph.
The only thing that we have to do is to call the function write on a file stream with the tag DotDrawing() and pass over our graph g.
FILE* strmWrite = fopen("graph.dot", "w");
write(strmWrite, g, DotDrawing());
fclose(strmWrite);
After executing this example, there should be a file graph.dot in your directory.
Alternatively, you can use the standard output to print the graph to the screen:
std::cout << g << '\n';
Assignment 1¶
- Type
- Review
- Objective
- Copy the code from above and adjust it such that a road trip from Berlin via Hamburg and Hannover to Munich is simulated.
- Hints
- Use directed Edges
- Solution
Click more... to see the solution.
#include <iostream> #include <seqan/graph_types.h> #include <seqan/graph_algorithms.h> using namespace seqan; int main () { typedef unsigned int TCargo; typedef Graph<Directed<TCargo> > TGraph; typedef VertexDescriptor<TGraph>::Type TVertexDescriptor; TGraph g; TVertexDescriptor vertBerlin = addVertex(g); TVertexDescriptor vertHamburg = addVertex(g); TVertexDescriptor vertHannover = addVertex(g); TVertexDescriptor vertMuenchen = addVertex(g); addEdge(g, vertBerlin, vertHamburg, 289u); addEdge(g, vertHamburg, vertHannover, 289u); addEdge(g, vertHannover, vertMuenchen, 572u); FILE* strmWrite = fopen("graph.dot", "w"); write(strmWrite, g, DotDrawing()); fclose(strmWrite); typedef Iterator<TGraph, VertexIterator>::Type TVertexIterator; TVertexIterator itV(g); std::cout << g << std::endl; return 0; }
Assignment 2¶
- Type
- Application
- Objective
- Write a program which creates a directed graph with the following edges: (1,0), (0,4), (2,1), (4,1), (5,1), (6,2), (3,2), (2,3), (7,3), (5,4), (6,5), (5,6), (7,6), (7,7) Use the function addEdges instead of adding each edge separately. Output the graph to the screen.
- Solution
Click more... to see the solution.
We first have to include the corresponding header file for graphs. Instead of <seqan/graph_types.h>, we can also include <seqan/graph_algorithms.h> as it already includes <seqan/graph_types.h>.
#include <iostream> #include <seqan/graph_algorithms.h> using namespace seqan;
This time we define a DirectedGraph without cargo at the edges.
int main() { typedef Graph<Directed<> > TGraph; typedef VertexDescriptor<TGraph>::Type TVertexDescriptor; typedef EdgeDescriptor<TGraph>::Type TEdgeDescriptor; typedef Size<TGraph>::Type TSize;
The function addEdges takes as parameters an array of vertex descriptors and the number of edges. The array of vertex descriptors is sorted in the way predecessor1, successor1, predecessor2, successor2, ...
TSize numEdges = 14; TVertexDescriptor edges[] = {1,0, 0,4, 2,1, 4,1, 5,1, 6,2, 3,2, 2,3, 7,3, 5,4, 6,5, 5,6, 7,6, 7,7}; TGraph g; addEdges(g, edges, numEdges); std::cout << g << std::endl;
The screen output of the graph consists of an adjacency list for the vertices and an edge list:
Adjacency list: 0 -> 4, 1 -> 0, 2 -> 3,1, 3 -> 2, 4 -> 1, 5 -> 6,4,1, 6 -> 5,2, 7 -> 7,6,3, Edge list: Source: 0,Target: 4 (Id: 1) Source: 1,Target: 0 (Id: 0) Source: 2,Target: 3 (Id: 7) Source: 2,Target: 1 (Id: 2) Source: 3,Target: 2 (Id: 6) Source: 4,Target: 1 (Id: 3) Source: 5,Target: 6 (Id: 11) Source: 5,Target: 4 (Id: 9) Source: 5,Target: 1 (Id: 4) Source: 6,Target: 5 (Id: 10) Source: 6,Target: 2 (Id: 5) Source: 7,Target: 7 (Id: 13) Source: 7,Target: 6 (Id: 12) Source: 7,Target: 3 (Id: 8)
Assignment 3¶
- Type
- Transfer
- Objective
Write a program which defines an HMM for DNA sequences:
Define an exon, splice, and intron state.
Consider to use the type LogProb<> from <seqan/basic/basic_logvalue.h> for the transition probabilities. Sequences always start in the exon state. The probability to stay in an exon or intron state is 0.9. There is exactly one switch from exon to intron. Between the switch from exon to intron state, the HMM generates exactly one letter in the splice state. The sequence ends in the intron state with a probability of 0.1.
Output the HMM to the screen.
Use the follwing emission probabilities.
A C G T exon state 0.25 0.25 0.25 0.25 splice state 0.05 0.0 0.95 0.0 intron state 0.4 0.1 0.1 0.4
- Solution
The program starts with the inclusion of <seqan/graph_algorithms.h> and <seqan/basic/basic_logvalue.h>. In this example you could include <seqan/graph_types.h> instead of the algorithms header file. However, it is likely that if you define a graph, you will call a graph algorithm as well.
#include <iostream> #include <seqan/graph_algorithms.h> #include <seqan/basic/basic_math.h> using namespace seqan;
Next, we define our types. The most interesting type here is THmm. It is a Graph with the specialization HmmGraph. The specialization takes itself three template arguments: the alphabet of the sequence that the HMM generates, the type of the transitions, and again a specialization. In our case, we define the transitions to be the logarithm of the probilities (LogProb) and hereby simplify multiplications to summations. For the specialization we explicitly use the Default tag.
int main() { typedef LogProb<> TProbability; typedef Dna TAlphabet; typedef Size<TAlphabet>::Type TSize; typedef Graph<Hmm<TAlphabet, TProbability, Default> > THmm; typedef VertexDescriptor<THmm>::Type TVertexDescriptor; typedef EdgeDescriptor<THmm>::Type TEdgeDescriptor;
After that, we define some variables, especially one of our type THmm.
Dna dnaA = Dna('A'); Dna dnaC = Dna('C'); Dna dnaG = Dna('G'); Dna dnaT = Dna('T'); THmm hmm;
Now we can start with defining the states. States are represented by the vertices of the HMM-specialized graph.
The initial and terminating states of an HMM in SeqAn are always silent, i.e. they do not generate characters. That is why we have to define an extra begin state and tell the program that this is the initial state of the HMM. The latter is done by calling the function assignBeginState.
TVertexDescriptor begState = addVertex(hmm); assignBeginState(hmm, begState);
For our three main states we also add a vertex to the HMM with addVertex. Additionally, we assign the emission probabilities for all possible characters of our alphabet using emissionProbability.
TVertexDescriptor exonState = addVertex(hmm); emissionProbability(hmm, exonState, dnaA) = 0.25; emissionProbability(hmm, exonState, dnaC) = 0.25; emissionProbability(hmm, exonState, dnaG) = 0.25; emissionProbability(hmm, exonState, dnaT) = 0.25; TVertexDescriptor spliceState = addVertex(hmm); emissionProbability(hmm, spliceState, dnaA) = 0.05; emissionProbability(hmm, spliceState, dnaC) = 0.0; emissionProbability(hmm, spliceState, dnaG) = 0.95; emissionProbability(hmm, spliceState, dnaT) = 0.0; TVertexDescriptor intronState = addVertex(hmm); emissionProbability(hmm, intronState, dnaA) = 0.4; emissionProbability(hmm, intronState, dnaC) = 0.1; emissionProbability(hmm, intronState, dnaG) = 0.1; emissionProbability(hmm, intronState, dnaT) = 0.4;
Finally, we need to define the end state and call assignEndState.
TVertexDescriptor endState = addVertex(hmm); assignEndState(hmm, endState);
For the HMM, only the transition probabilities are still missing. A transition is represented by an edge of our HMM graph type. The cargo on these edges correspond to the transition probabilities.
Since the sequences always start with an exon, we set the transition probability from the begin state to the exon state to 1.0 calling the already well-known function addEdge. And also the other transitions can be defined in the same way.
addEdge(hmm, begState, exonState, 1.0); addEdge(hmm, exonState, exonState, 0.9); addEdge(hmm, exonState, spliceState, 0.1); addEdge(hmm, spliceState, intronState, 1.0); addEdge(hmm, intronState, intronState, 0.9); addEdge(hmm, intronState, endState, 0.1);
To check the HMM we can simply output it to the screen:
std::cout << hmm << '\n';
This should yield the following:
Alphabet: {A,C,G,T} States: {0 (Silent),1,2,3,4 (Silent)} Begin state: 0 End state: 4 Transition probabilities: 0 -> 1 (1.000000) 1 -> 2 (0.100000) ,1 (0.900000) 2 -> 3 (1.000000) 3 -> 4 (0.100000) ,3 (0.900000) 4 -> Emission probabilities: 1: A (0.250000) ,C (0.250000) ,G (0.250000) ,T (0.250000) 2: A (0.050000) ,C (0.000000) ,G (0.950000) ,T (0.000000) 3: A (0.400000) ,C (0.100000) ,G (0.100000) ,T (0.400000)
Property Maps And Iterators¶
So far, the vertices in our graph can only be distinguished by their vertex descriptor. We will now see how to associate the city names with the vertices.
SeqAn uses External Property Map to attach auxiliary information to the vertices and edges of a graph. The cargo parameter that we used above associated distances to the edges. In most scenarios you should use an external property map to attach information to a graph. Be aware that the word external is a hint that the information is stored independently of the graph and functions like removeVertex do not affect the property map. Property maps are simply Strings of a property type and are indexed via the already well-known vertex and edge descriptors.
Lets see how we can define a vertex property map for the city names. Our property type is a String of a city name type, a char string. We only have to create and resize this map so that it can hold information on all vertices.
typedef String<char> TCityName;
typedef String<TCityName> TProperties;
TProperties cityNames;
resizeVertexMap(g, cityNames);
Next, we can enter the city names for each vertex. Note that this is completely independent from our graph object g.
assignProperty(cityNames, vertBerlin, "Berlin");
assignProperty(cityNames, vertHamburg, "Hamburg");
assignProperty(cityNames, vertMuenchen, "Munich");
assignProperty(cityNames, vertMainz, "Mainz");
assignProperty(cityNames, vertHannover, "Hannover");
If we now want to output all vertices including their associated information we can iterate through the graph and use the iterators value to access the information in the property map.
But let us first have a quick look at iterators for graph types. SeqAn provides six different specializations for graph iterators: Vertex Iterator, Adjacency Iterator, Dfs Preorder Iterator, and Bfs Iterator for traversing vertices, and Edge Iterator and Out-edge Iterator for traversing edges. Except for the Vertex Iterator and the Edge Iterator they depend additionally to the graph on a specified edge or vertex.
To output all vertices of our graph in an arbitrary order, we can define an iterator of the specialization Vertex Iterator and determine its type with the metafunction Iterator. The functions atEnd and goNext also work for graph iterators as for all other iterators in SeqAn.
The value of any type of vertex iterator is the vertex descriptor. To print out all city names we have to call the function getProperty on our property map cityNames with the corresponding vertex descriptor that is returned by the value function.
typedef Iterator<TGraph, VertexIterator>::Type TVertexIterator;
TVertexIterator itV(g);
for(;!atEnd(itV);goNext(itV)) {
std::cout << value(itV) << ':' << getProperty(cityNames, value(itV)) << std::endl;
}
The output of this piece of code should look as follows:
0:Berlin
1:Hamburg
2:Hannover
3:Mainz
4:Munich
Assignment 4¶
- Type
- Application
- Objective
Add a vertex map to the program from task 2:
- The map shall assign a lower-case letter to each of the seven vertices. Find a way to assign the properties to all vertices at once in a single function call (without using the function assignProperty for each vertex separately).
- Show that the graph is not connected by iterating through the graph in depth-first-search ordering. Output the properties of the reached vertices.
- Solution
Our aim is not to assign all properties at once to the vertices. Therefore, we create an array containing all the properties, the letters ‘a’ through ‘h’.
The function assignVertexMap does not only resize the vertex map (as resizeVertexMap does) but also initializes it. If we specify the optional parameter prop, the values from the array prop are assigned to the items in the property map.
String<char> nameMap; char names[] = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'}; assignVertexMap(g,nameMap, names);
To iterate through the graph in depth-first-search ordering we have to define an Iterator with the specialization DfsPreorderIterator.
The vertex descriptor of the first vertex is 0 and we choose this vertex as a starting point for the depth-first-search through our graph g with the iterator dfsIt:
TVertexDescriptor start = 0; typedef Iterator<TGraph, DfsPreorder>::Type TDfsIterator; TDfsIterator dfsIt(g, start); std::cout << "Iterate from '" << getProperty(nameMap, start) << "' in depth-first-search ordering: "; while(!atEnd(dfsIt)) { std::cout << getProperty(nameMap, getValue(dfsIt)) << ", "; goNext(dfsIt); } std::cout << std::endl;
For the chosen starting point, only two other vertices can be reached:
Iterate from 'a' in depth-first-search ordering: a, e, b,
Graph Algorithms¶
Now that we completed creating the graph we can address the graph algorithms. Here is an overview of some graph algorithms currently available in SeqAn:
- Elementary Graph Algorithms
- Breadth-First Search (breadthFirstSearch)
- Depth-First Search (depthFirstSearch)
- Topological Sort (topologicalSort)
- Strongly Connected Components (stronglyConnectedComponents)
- Minimum Spanning Tree
- Prim’s Algorithm (primsAlgorithm)
- Kruskal’s Algorithm (kruskalsAlgorithm)
- Single-Source Shortest Path
- DAG Shortest Path (dagShortestPath)
- Bellman-Ford (bellmanFordAlgorithm)
- Dijkstra (dijkstra)
- All-Pairs Shortest Path
- All-Pairs Shortest Path (allPairsShortestPath)
- Floyd Warshall (floydWarshallAlgorithm)
- Maximum Flow
- Ford-Fulkerson (fordFulkersonAlgorithm)
- Transitive Closure
- Transitive Closure (transitiveClosure)
- Bioinformatics Algorithms
- Needleman-Wunsch (globalAlignment)
- Gotoh (globalAlignment)
- Hirschberg with Gotoh (globalAlignment)
- Smith-Waterman (localAlignment)
- Multiple Sequence Alignment (globalMsaAlignment)
- UPGMA (upgmaTree)
- Neighbor Joining (njTree)
The biological algorithms use heavily the alignment graph. Most of them are covered in the tutorial Alignment Representation. All others use the appropriate standard graph. All algorithms require some kind of additional input, e.g., the Dijkstra algorithm requires a distance property map, alignment algorithms sequences and a score type and the network flow algorithm capacities on the edges.
Generally, only a single function call is sufficient to carry out all the calculations of a graph algorithm. In most cases you will have to define containers that store the algorithms results prior to the function call.
In our example, we apply the shortest-path algorithm of Dijkstra. It is implemented in the function dijkstra.
Let’s have a look at the input parameters. The first parameter is of course the graph, g. Second, you will have to specify a vertex descriptor. The function will compute the distance from this vertex to all vertices in the graph. The last input parameter is an edge map containing the distances between the vertices. One may think that the distance map is already contained in the graph. Indeed this is the case for our graph type but it is not in general. The cargo of a graph might as well be a string of characters or any other type. So, we first have to find out how to access our internal edge map. We do not need to copy the information to a new map. Instead we can define an object of the type InternalMap of our type TCargo. It will automatically find the edge labels in the graph when the function property or getProperty is called on it with the corresponding edge descriptor.
The output containers of the shortest-path algorithm are two property maps, predMap and distMap. The predMap is a vertex map that determines a shortest-paths-tree by mapping the predecessor to each vertex. Even though we are not interested in this information, we have to define it and pass it to the function. The distMap indicates the length of the shortest path to each vertex.
typedef Size<TGraph>::Type TSize;
InternalMap<TCargo> cargoMap;
String<TVertexDescriptor> predMap;
String<TSize> distMap;
Having defined all these property maps, we can then call the function dijkstra:
dijkstra(g,vertHannover,cargoMap,predMap,distMap);
Finally, we have to output the result. Therefore, we define a second vertex iterator itV2 and access the distances just like the city names with the function property on the corresponding property map.
TVertexIterator itV2(g);
while(!atEnd(itV2)) {
std::cout << "Shortest path from " << property(cityNames, vertHannover) << " to " << property(cityNames, value(itV2)) << ": ";
std::cout << property(distMap, value(itV2)) << std::endl;
goNext(itV2);
}
return 0;
}
Assignments 5¶
- Type
- Application
- Objective
- Write a program which calculates the connected components of the graph defined in task 1. Output the component for each vertex.
- Solution
SeqAn provides the function stronglyConnectedComponents to compute the connected components of a directed graph. The first parameter of this function is of course the graph. The second parameter is an output parameter. It is a vertex map that will map a component id to each vertex. Vertices that share the same id are in the same component.
String<unsigned int> component; stronglyConnectedComponents(g, component);
Now, the only thing left to do is to walk through our graph and ouput each vertex and the corresponding component using the function getProperty. One way of doing so is to define a VertexIterator.
std::cout << "Strongly Connected Components: " << std::endl; typedef Iterator<TGraph, VertexIterator>::Type TVertexIterator; TVertexIterator it(g); while(!atEnd(it)) { std::cout << "Vertex " << getProperty(nameMap, getValue(it)) << ": "; std::cout << "Component = " << getProperty(component, getValue(it)) << std::endl; goNext(it); } return 0; }
The output for the graph defined in the Assignment 4 looks as follows:
Strongly Connected Components: Vertex a: Component = 3 Vertex b: Component = 3 Vertex c: Component = 2 Vertex d: Component = 2 Vertex e: Component = 3 Vertex f: Component = 1 Vertex g: Component = 1 Vertex h: Component = 0
The graph consists of four components. The first contains vertex a, b, and e, the second contains vertex c and d, the third contains vertex f and g and the last contains only vertex h.
Assignment 6¶
- Type
- Application
- Objective
Extend the program from the Assignment 5. Given the sequence s = "CTTCATGTGAAAGCAGACGTAAGTCA".
- calculate the Viterbi path of s and output the path as well as the probability of the path and
- calculate the probability that the HMM generated s with the forward and backward algorithm.
- Solution
In Assignment 3 we defined an HMM with three states: exon, splice, and intron.
The Viterbi path is the sequence of states that is most likely to produce a given output. In SeqAn, it can be calculated with the function viterbiAlgorithm. The produced output for this assignment is the DNA sequence s.
The first parameter of the function viterbiAlgorithm is of course the HMM, and the second parameter is the sequence s. The third parameter is an output parameter that will be filled by the function. Since we want to compute a sequence of states, this third parameter is a String of VertexDescriptors which assigns a state to each character of the sequence s.
The return value of the function viterbiAlgorithm is the overall probability of this sequence of states, the Viterbi path.
The only thing left is to output the path. The path is usually longer than the given sequence. This is because the HMM may have silent states, e.g. the begin and end state. To check if a state is silent SeqAn provides the function isSilent.
String<Dna> sequence = "CTTCATGTGAAAGCAGACGTAAGTCA"; String<TVertexDescriptor> path; TProbability p = viterbiAlgorithm(hmm, sequence, path); std::cout << "Viterbi algorithm" << std::endl; std::cout << "Probability of best path: " << p << std::endl; std::cout << "Sequence: " << std::endl; for(TSize i = 0; i < length(sequence); ++i) std::cout << sequence[i] << ','; std::cout << std::endl; std::cout << "State path: " << std::endl; for(TSize i = 0; i < length(path); ++i) { std::cout << path[i]; if (isSilent(hmm, path[i])) std::cout << " (Silent)"; if (i < length(path) - 1) std::cout << ','; } std::cout << std::endl;
The output of the above piece of code is:
Viterbi algorithm Probability of best path: 1.25465e-18 Sequence: C,T,T,C,A,T,G,T,G,A,A,A,G,C,A,G,A,C,G,T,A,A,G,T,C,A, State path: 0 (Silent),1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,3,3,3,3,3,3,3,4 (Silent)
It is even simpler to use the forward algorithm in SeqAn since it needs only the HMM and the sequence as parameters and returns a single probability. This is the probability of the HMM to generate the given sequence. The corresponding function is named forwardAlgorithm.
std::cout << "Forward algorithm" << std::endl; p = forwardAlgorithm(hmm, sequence); std::cout << "Probability that the HMM generated the sequence: " << p << std::endl;
Analogously, the function backwardAlgorithm implements the backward algorithm in SeqAn.
std::cout << "Backward algorithm" << std::endl; p = backwardAlgorithm(hmm, sequence); std::cout << "Probability that the HMM generated the sequence: " << p << std::endl; return 0; }
The output of these two code fragments is:
Forward algorithm Probability that the HMM generated the sequence: 2.71585e-18 Backward algorithm Probability that the HMM generated the sequence: 2.71585e-18